• Pressure
• Temperature
• R, the Gas Constant
• A Few Gas Laws
• Back to Stoich
• Kinetic Molecular Theory of Gases
• Effusion and Diffusion
• An Alternative to the Ideal Gas Law

This is a different section. The sections before this just built upon each other, all having to do with chemicals and reactions and formulas. The first part of this chapter will have almost nothing to do with that. Then of course, we must tie it back in. But it's a good break from stoich, you must agree.

Before anything, I hope I don't have to define "gas" for you. Well, just in case, a gas is a substance that doesn't have a definite shape nor volume. Obviously gases will form the shape of their container. And their volume is simply the volume of the container they're in.

Pressure

Gases push and expand. It's in their nature. That's why they will evetually take the shape of their container: they push and expand, hitting the walls and being stopped. That's because gases have particles that have lots of motion, flying around, in comparison to solids, whose molecules are almost fixed. Gases push against the walls of their container, with pressure. Pressure is defined as a force per unit area. It is simply not enough to say how much it pushes, but also how much surface area it is pushing on.

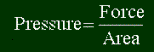
For example, if you press a book against your hand with a relatively strong force, it doesn't hurt. That force is acting on a large area, so you don't feel much pressure. But what would happen if you push a needle pointwise first into your hand, with the same force? You will definitely feel a pressure. Because that force is acting on a very small area, the pressure will be greater.

You can easily see the pressure by a gas in a balloon. The reason it stays round is because the gas inside is under pressure, pushing at the walls in every direction. If you try to squeeze it, you can feel the gases' pressure increasing, pushing against you. (That's one of the gas laws.)

So what are units of pressure? Pressure is force divided by area, or newtons per square meter. The SI system doesn't like to have different units' names in other units, so they call a newton per square meter a pascal (Symbol: Pa). So 1 pascal of pressure is equal to a force of 1 newton pressing down on a square meter. If you don't know force, a newton is pretty small. Imagine a small force delivered to a relatively big area of 1 m². A pascal is very small. A more common unit is the kilopascal (Symbol: kPa). Obviously 1 kPa = 1000 Pa.

That's the SI version. Obviously, here in the great United States, we like to use different units that run different to the rest of the world, and pressure is no exception. We use pounds per square inch (Symbol: psi), which is the same concept as the pascal, just with different units. More common units to use in chemistry are the torr and the atmosphere. To discuss any of these requires a discussion of atmospheric pressure:

Air doesn't weigh much. Yet it does have a little weight. Look at all the air above us. There's a ton of it in the atmosphere. It's hard to imagine all that air, and that we don't feel it crushing us down. Air does weigh a lot. But since it's force is spread out over such a large surface as the earth, it's not as much. Still, the pressure is equal to about 101325 pascals, or almost 15 pounds per square inch. That means that a force on a 8.5 by 11 inch piece of paper should be almost 1400 pounds! How come we don't feel all this atmosphere pressure? Because it acts in all directions. That piece of paper feels 15 psi pushing down, pushing up, pushing left, pushing right, pushing in all directions. So the net force, and pressure, is zero. The point is, wherever there is air, it will be pushing at 15 psi in all directions. So, let's take a can. There is air inside and outside a can, and the air inside is pushing outward at 15 psi, and the air outside is pushing inward at 15 psi, and the can doesn't implode nor explode.

Would the atmospheric pressure be greater or less at higher altitudes than at lower altitudes? Well, as you go up, there is less and less air pushing down on you, since a lot of it is now below you. So air pressure will decrease as you go up. That's why they pressurize air inside an airplane, to keep the pressure at normal 15 psi inside, while it's much lower outside. If you thought someone could open the door of the plane, it would take a couple of tons of force to get that door open. Plane doors swing inward, and the much greater pressure on the inside would oppose the door moving in.

One more thing about atmospheric pressure: why vacuums suck. If you have a hollow cube, and the air is taken out of the middle, you have an enormous force crushing all sides of the cube. If you make a tiny hole in this cube, then all this air will try to rush in, because it pushes, and you get a sucking effect.

Anyway, I hope you get what atmospheric pressure is. They named a unit of pressure after it, appropriately called the atmosphere (Symbol: atm). 1 atm is equal to the pressure of the atmosphere, at sea level. So, 1 atm = 101325 Pa. To explain torrs (or mmHg, same thing), we must set up a lab.

Fill a dish with some mercury. Fill a tube completely with mercury. Turn this tube really quickly upside down into this dish. Let's see what happens:

This is how it looks like. Immediately after you flip it, the mercury will want to fall out of the tube, due to gravity. But, there is one force acting on the liquid that will oppose that: atmospheric pressure. It is pushing on the surface of the liquid, and pushing the column back up, like so:

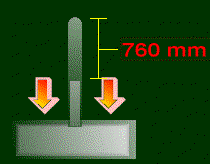
Those arrows are pushing on the liquid, and forcing the column to go back inside the tube. These two forces on the column will come to an equilibrium (they will balance). The result: the distance between the top to the tube and the top of the mercury is always 76.0 cm (or more commonly in mm, 760 mm), at least at sea level. That is the concept of the mm Hg (pronounced millimeters of mercury): 1 mm Hg is the amount of pressure that would make that column of vacuum above the mercury be 1 mm tall. Therefore, the atmospheric pressure is 760 mm Hg. Also, another name for mm Hg is the torr. Just another way of saying it. So 1 mmHg = 1 torr.

There are other units of pressure, like bars or mm H₂O, but they aren't used commonly, at least not in chemistry. So that's about it for pressure. It will come back to haunt you later, in fact, probably in the next section. So beware!

Temperature

You might feel silly to be reading about temperature. You know what it is. It's how hot or cold something is. But in terms of particles and chemistry and such, what exactly is temperature? It's a measure of the average kinetic energy of the particles in a gas. What is kinetic energy? The definition is as follows:

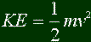
m stands for mass, and v stands for velocity. So if something is moving faster than before, it will have more kinetic energy than before. And so temperature is really the measure of how fast the particles are moving around. (You generally ignore the mass part of it in temperature, since particles are known to change speed but usually not mass... :)

So now you can see why if you heat a liquid enough, it will turn into a gas (evaporate). As it gets an increase in temperature, its getting an increase in kinetic energy (and speed of particles). If you get high enough, the particles will be moving fast enough and be going crazy, and becomes a gas.

Note that temperature is a measure of the average kinetic energy of all the particles. Not all particles will be traveling at the same speed. But the average of the energies is related to the temperature.

There is no upper limit on temperature. You can always give something more and more energy, and the particles will just get faster and faster. There is a lower bound tho. Since the slowest a particle can move is 0 mph, temperature will be at its lowest when the particles are absolutely still. The temperature at which this theoretically happens is called absolute zero. This is very very very cold, much more cold than the coldest day in the North Pole. It's -459.67 ^oF, or -273.15 ^oC. You know, that's cold. This is the temperature at which all motion of particles will stop. This temperature has never been reached by anyone anywhere, but people have come close to it (within .00000001 ^oC or something). Wouldn't it make sense if we started a temperature scale that had this temperature as 0? So that we wouldn't need to deal with negative numbers? The Kelvin scale is the scale we need. The symbol is K (without the stupid circle; not ^oK.) 0 K is absolute zero. Therefore there are no negative Kelvins. The good thing is, 1 K = 1 ^oC. The Kelvin and the degree Celsius are the same unit, equal. The only thing different is where they start. So, converting is easy. Let's assume that we can round -273.15 to -273. This is the number commonly used to convert. All you do to the Celsius temperature is add 273 to it, and that's how many Kelvins you have. A quick few examples:

• 0 ^oC = 273 K.
• 10 ^oC = 283 K.
• -30 ^oC = 243 K.
• 100 ^oC = 373 K.

You get the idea. And to go the other way; if you wanted Celsius from Kelvin, just subtract 273. You generally don't do that, unless a question asked for units of Celsius or something.

Why go through all this? What was wrong with the Celsius system, it never failed us! But it did, because the numbers weren't proportional. Something at 20 degrees Celsius did not have twice as much kinetic energy as something at 10 degrees Celsius. Back when they invented the Celsius and Fahrenheit scales, they had no idea that there was a bottom of the scale. They thought it went infinite in both directions. So they just picked a temperature and called it zero. (For celsius, it was the freezing point of water.) But with the Kelvin scale, you can truly say that something at 20 K has twice as much kinetic energy as something at 10 K. All of the equations that involve temperature in this section will need to be in Kelvins. So remember to convert!

And one last note: I always said that temperature was related to the average kinetic energy, but not exactly how. Here is the equation (you'll probably never use it, but if you're interested... knock yourself out.)

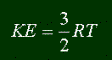
KE is the average kinetic energy, T is temperature (in Kelvins of course!) and R is...well...let's talk about that next.

R, the Gas Constant

R is a gas constant. It has a constant value. It's used in many equations. There are two forms of this constant (meaning different units). There's a version that involes energy, and the version that involves volume and pressure. Learn to use which one in each equation! (For example, since the equation above in the last section had energy, but not pressure nor volume, you would use the energy form.)

Pressure-Volume form:

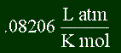
Energy form:

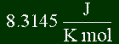
In case you don't have a graphics browser, the pressure-volume form is .08206 L atm / (K mol), and the energy form is 8.3145 J / K mol. These two values are exactly the same, they are just used in different equations.

A Few Gas Laws

There are laws all over in science. There just so happens that gases must follow some laws of their own. Let us go over some relationships between some properties of gases.

Boyle's Law

This law says: The pressure and the volume of a gas are inversly proportional to each other, temperature kept constant. What this means, is that if you keep the temperature constant, then if you increase the pressure on the gas, the volume will decrease, and if you lessen the pressure on a gas, the volume will increase.

If you crush a gas, it's gonna shrink.

Real world example: that balloon thing again. If you squeeze a balloon enough, it pushes back, until the gas is too pressurized and the balloon pops. Bigger balloons are easier to squeeze. (Note: I don't know anything about squeezing balloons. I have never done it. I'm just assuming this stuff, because it's the only example I could think of. If I am misinformed about balloon squeezing, please tell me and I will fix it, hehe.)

Boyle's Law can be expressed like this: for every gas, assuming temperature is constant, there exists a constant, say, b, and this equation will hold true for all values of P and V obtained simultaneously: b = P / V.

Believe it or not, you can do some example problems with this!

Example:

Charles's Law

This law says: The temperature and the volume of a gas are directly proportional, assuming pressure is kept constant. That means as the temperature goes up, the volume will go up as well.

This is easy to picture. If the temperature goes up, the particles get faster, and they want to move outward more. The gas expands, and the space it takes up increases. The opposite also happens; if temperature is lowered, volume will be less.

This is easily observed in a hot air balloon. To make a balloon go up, they light a fire inside of it. This will heat up the gas inside the balloon. So the volume will go up. Since mass stays the same, the density of the air inside will become less. The reason a balloon floats is because the air inside is less dense than the air outside. Wow...

Just as we could write Boyle's Law with some sort of equation, you can write Charles's Law too.

For every gas there exists a constant, say, d, at which V = dT, pressure being held constant.

So here are some examples! (Actually, just one.)

Example:

So Boyle's Law and Charles's Law have to do with relationships between different properties of gases, how they vary with each other. There is one more, and this one's easy: Avogadro's Law.

Avogadro's Law

This one is easy: the moles of gas is directly proportional to the volume. Easy; if you have twice as many moles of gas, it will take up twice as much space, assuming you keep that other crap constant (such as pressure and temperature).

This also leads to something interesting. Before we go into this "interesting" thing, I introduce to you STP. Standard Temperature and Pressure. When a gas is at STP, it is understood that it is at O ^oC, and at 1 atm.

Now for the interesting thing. At STP, one mole of gas, any gas, will occupy exactly 22.4 liters. Doesn't matter how big the particles are, and such.

If you must need an example on this law...well...hrm...you suck!

Combining Boyle's and Charles's Laws

This one is combining volume, pressure and temperature into one easy equation to remember. It is pronounced, "Vopotin equals Vinpinto", and you can find one of them, given the other five. The equation is written as follows.

V_oP_oT_N = V_NP_NT_o

This is one step below the almighty Ideal Gas Law. Try a problem out with this:

Example:

Dalton's Law of Partial Pressures

This is the easiest law. The pressures of gases are additive. If you put a gas at A atms into a container, and then put another gas of B atms into it, then the total pressure in that container is A + B. Now it's time for the big daddy of all Gas Laws...the Ideal Gas Law.

Ideal Gas Law

Well, here it comes, the law that will tie it all together: the Ideal Gas Law. It ties in all the quantities together we have discussed so far, and a simple and easy-to-memorize equation is what you get.

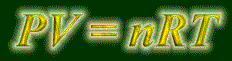
(Sorry for overdoing the pic!)

This equation is called "Piv-Nert". That is how you pronounce it. You will be using this for many many things, so get used to it! Basically, this equation will let you find the property that you don't know, given that you know the other three.

P - pressure (in atms).

V - volume (in liters).

n - quantity of gas (in moles).

R - the gas constant discussed earlier. Hopefully, you recognize this R as being the pressure-volume form, and is therefore .08206 L atm / K mol.

T - temperature, IN KELVINS!!! The biggest mistake people make early on is forgetting to convert to Kelvins. So do it!

And that is it. This equation is probably most useful for finding the moles of gas, since all the other quantities can be measured easily. Pressure is found by some kind of gauge, volume is simply the volume of the container, and temperature can be found with a thermometer (I hope you knew that.)

I won't give any examples, because you can do plug-'n'-chug, and because any other problem that might require some tinkering with the Ideal Gas Law can be easily solved with the VoPoTn = VnPnTo equation.

Note that this is called the "Ideal" Gas Law. Real gases don't exactly follow this law, mostly because the pressure and volume aren't as they seem to be. So what is an ideal gas? There isn't such a thing in the real world, it's simply a model that tries to mimic experiment data as much as possible, and still be simple. Let's go back and see what's wrong with this model.

Pressure. The Ideal Gas Law assumes that there are no interactions between molecules. They just bounce around, with some kinetic energy. But in reality, the molecules are attracted to each other. Therefore, they wouldn't be hitting the walls of the container as hard as are expected. Therefore the actual pressure will be greater than the observed pressure.

Volume. The Ideal Gas Law assumes that the molecules are points that don't take any actual space themselves. But in reality...molecules take up space!!! (Don't act surprised.) So the actual volume that is there is less than what is observed, since the molecules take some space up which the gas should be taking up according to the Ideal Gas Law.

These factors will be taken into consideration when coming up with a more realistic gas law.

Back to Stoich

I'm so sorry, but we do have to return back to the world of moles and LRs and formulas. It was a good break from it tho. This section will not teach you anything new, just help you connect stoich and this new junk you had to learn. The key is...moles!!! Stoich is always about the moles. So if you get something in grams... convert to moles! If you get a volume, pressure, and temperature... use Pivnert to get moles!

Here's a typical problem you might have to do.

Example:

Here's a special formula. Nothing out of the ordinary, just derived from the Ideal Gas Law. It's how to find the molar mass of the gas, given pressure, temperature, and density.

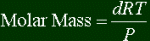
d is density, in grams per liter, instead of milliliter, because R has liters in it.

There's some things to notice in this. If the temperature goes up of a gas, then density goes down. That's how a hot air balloon works, by decreasing the density of the gas inside by increasing temperature.

Mole fractions. I thought I mentioned them before, looks like I didn't. This is how much a mixture is made up of a particular gas. The symbol for it is a greek 'x' thing, like X. It's very easy. Let's say you have x moles of gas A, and y moles of gas B put together. The mole fraction of gas A will be:

x moles
-------------------------
Total moles (x + y)

It's like a percentage, but you don't multiply by 100. Mole fractions have no units, since mol cancels out.

Quikie: You have 2 moles of helium mixed with 5 moles of xenon. The mole fraction of helium is 2 moles / (2 moles + 5 moles) = 2/7, or 0.286. The mole fraction of xenon is .714. Note that all the mole fractions of all the gases making up a mixture must add up to 1. (Just like all percentages add up to 100%). You can think of the mole fraction as the probability of picking up one random particle and getting that gas.

Now, the cool thing is that pressure and mole fraction are related. When two or more gases are put together in the same container, their mole fractions are proportional to the pressures, and vice-versa. Why? Because when gases are put together, their volumes are the same, and so is their temperatures. The only thing that is different is their pressures and mole fractions, and so they are proportional.

What does this mean for you? It means you can do stupid little problems like... (Two gases, with .432 and .568 for mole fractions, have a total combined pressure of 3.00 atms. What is the pressure of each gas?)

Note that the pressures of the individual gases added together will be the total pressure observed, because of Mr. Dalton's law.

Let's talk about vapor pressure, since it is needed in some problems.

Vapor Pressure

Let's say you want to collect the gas of a reaction. One way of doing this is like so:

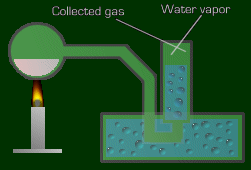
You let the gas bubble out to the top, and there's a little space above the water where the gas will reside. One very important thing to realize is that the pressure of the 'stuff' above there isn't the pressure of the gas being collected. There is also water vapor in that space, which is contributing to the pressure.

You say, 'Where is this vapor coming from?' From the water, of course! This means the pressure observed is greater than the actual pressure of the gas being collected, since the pressure measured includes both the water vapor pressure and the gas pressure.

So what do you do? You will get the pressure of water vapor as a given, with the problem. Then just take the pressure you measured, and subtract the water vapor pressure. And there's your true pressure of the gas.

I'm very sorry for the lack of examples in this section, since that is what it was intended for; to help you solve problems. But the truth is, it's very hard to make up a problem without copying it from the book, and I don't like to do that. Plus, it's hard on the fingers. Maybe when this whole page is done, I will come back and do these. Of course, by then, you will have graduated college and wouldn't care, would you?

Kinetic Molecular Theory of Gases

The Kinetic Molecular Theory of Gases (henceforth the "KMT") is the model we've been using, in these Laws, including Ideal Gas Law. It's a model, which tries to mimic real-world observations as much as possible, but also keeping it simple. As a result, you get a really simple equation to work with, but it makes some assumptions that aren't really true. Here is what this model is assuming:

• The molecules of gas don't take up any volume. They are simply points of mass.
• The molecules are always moving, and the average of the energy is related to temperature.
• The molecules don't have any forces exerted upon each other.

These are wrong! But... they can be ignored, resulting in a formula that actually does a good job of predicting gases in the real world, at least in certain situations.

Now my book goes through the trouble of deriving the Ideal Gas Law, but I don't want to bother you. You can thank me later.

Perhaps the only thing you might need to know is the root mean square velocity. This equation will give you the average of the squares of the speeds of the particles. This can be easily derived, since you know the mass of a particle, and the energy (you learned the equation way back up there). Here it is:

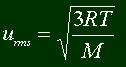
Capital M? Doesn't this mean molarity? Nope, not here. There are 26 letters, actually 52 both UPPER and lower, and almost as many Greek letters, and it's funny why they reuse the same letters... M means kilogram per mole. So just divide the molecular weight of a particle of gas by 1000.

Effusion and Diffusion

Tired of gases? We still have two quick topics to cover until you become a full-fledged PhD in AP Gases. Effusion and diffusion wasn't really covered in my class. They basically compare the rates at which gases travel from one place to another. This is only relative rates; you'll see more later.

Effusion is the rate at which particles will travel from one compartment to another totally empty compartment (vacuum), separated by only a small hole. To help ya visualize this, of course here's a visual (that's what they're for):

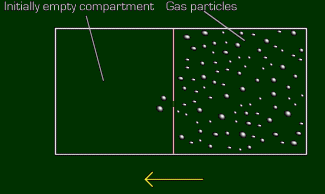
The particles go in the direction of that yellow arrow, towards the empty chamber. It does so at a constant rate, until they are balanced. Different gases will do this at different speeds. Generally, the lighter the particle is, the faster it will effuse. All right, all right, I'll stop yakking and just give you the formula, that's all you ingrates want anyway.

Note that this will not give you any rates. It will tell how much faster Gas A will effuse than Gas B. Note the capital 'M' again, meaning the kilograms per mole. But in this case, it doesn't really matter, since units cancel. Just keep molecular weight units consistent with both gases.

So let's find out how fast hydrogen gas will effuse compared to oxygen. Since hydrogen is lighter, we know that it will be faster, but by how much? Let's call hydrogen Gas B, since its rate will be on top on the left part. Therefore, helium's molecular weight will go on top on the right (note that it's flip-flopped?)

Rate of H₂ / Rate of O₂ = Ö(32 / 2) = 4.

This means hydrogen effuses 4 times as fast as oxygen.

Diffusion is when a gas travels across a distance. Like in a room, when someone farts at one end of the room, and it travels to the other end, it's diffusing. Some gases travel faster than others. Generally, lighter gases travel faster, and the whole concept is exactly the same as effusion. Same formula, that's good news 4 u.

An Alternative to the Ideal Gas Law

We already said that the Ideal Gas Law could be better, accounting for the fact that molecules take up space, and have attractions to each other. Well, here it comes. We know that we must subtract from volume, and add to pressure to account for those things. Therefore, here's the "real" (or at least better) Ideal Gas Law.

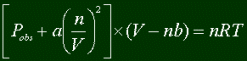
There are no new variables except for this 'a' and 'b'. They are constants that depend only on the identity of the gas. This formula will be more accurate than the Ideal Gas Law. The only thing is, you can't use them unless you are given the constants a and b. Once you do, tho, you can solve for anything. One thing, though, it's a bitch to solve for n, since it turns out to be a quadratic something-or-other. But, if you're smart like me, you already bought your TI-89, in which case you just plug it in :)

Congratulations! You're done with gases, and I'm done with gases too. Go try the practice problems now!