Stoichiometry
By TakalahTopics Covered
Stoich is short for stoichiometry. Don't be scared off by that name; I remembered in
ninth grade when I heard that I thought I wasn't going to get through the year. It's a
13-letter name for something that's very easy, yet important part to becoming successful
in chemistry. This is where the stuff becomes important to learn, because it's directly on
the test.
The Mole and Molar Calculations
I am surprised to hear that this is the point where some chemistry students lose all
hope; trying to figure out what a mole is. I admit, I was confused too, but keeping this
in mind made life a lot easier: a mole is simply the measure of how many. A similar unit
is a dozen, and since everyone knows what this is, I'll use this first.
Let's say you have a dozen eggs. What does this mean? It just means you have twelve of
something. It doesn't say how much it weighs, or how much space it occupies, just how
much. A dozen siege tanks doesn't have the same mass nor volume to a dozen specks of dust.
There's just twelve of each.
Moles are the same concept. One mole of something has 6.022 x 1023 objects
in it. It's a lot, but atoms are small, so it's a good unit in chem. 6.022 x 1023
is NA, called Avogadro's number. It's a pretty big number. One mole of seconds
is 4 million times as long as the age of the earth. One mole of meters is over 600 times
the diameter of the Milky Way. For our purposes, it's pretty good.
It's important to understand the relation of amu's and moles. One mole of something
that weighs one amu is one gram. In other words, 1 g = 6.022 x 1023 amus. So
one mole of hydrogen (H2) would weigh 1.0079 x 2 = 2.0158 grams. One mole of carbon is
exactly 12 grams; that's how they derived Avogadro's number.
Often it's important to find out how many moles is some given quantity of mass. You can
use dimensional analysis (DA) for this. Let's say you want to know how many moles is 36
grams of water, and also how many molecules are in it. First you must find the molar mass
of water (how many amus it weighs). Water is H2O, that means 2 of hydrogen and
one of oxygen. So the adding of those masses is:
1.008 x 2 + 16.00 = 18.00 amu.
Now comes the DA part.
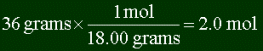
So it's 2 moles. And since 1 mole is NA molecules, there are 2 x NA
= 1.2 x 1024 molecules.
The key to solving these problems is getting the g/mol (molar mass, or amus) of the
substance, and then using that in a DA setup to convert back and forth between grams and
moles. One amu is one g/mol.
Example:
| How many moles are in 4.5 grams of glucose (C6H12O6)?
Answer
First you must find out the molar mass of glucose. Adding the weights of the individual
atoms, you get:
6 x 12.00 amu + 12 x 1.008 amu + 6 + 16.00 amu = 180.1 amus = 180.1 g/mol
Then you use DA:
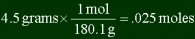
The answer is .025 moles. Be careful to use DA correctly, and that you will have to
flip it so that the units in the top and bottom cancel out. |
Example:
| You have a sample of glucose (C6H12O6), that weighs
2.5 grams. How many carbon molecules are in it? Answer
Find the number of moles of glucose (we already found molar mass of glucose in last
problem, 180.1.)
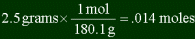
In each glucose molecule there are six carbons. So if you have .014 moles of glucose,
you must have 6 times as many carbons in it. .014 moles x 6 = .084 moles C. Just multiply
it by Avogadro's number to get the answer.
.084 moles x 6.022 x 1023=5.1 x 1022 carbon molecules. |
Percent Mass
This is just another way to show how much of something is in a compound. It's how much
of the substance is made of one particular element, the percent by mass (I bet you could
figure that out by the title). So if there is 60 g of something, and in that compound
there is 12 g of carbon, then you would say the percent mass is 20% (12 g / 60 g x 100%).
Note that this number can't be directly obtained from the moles. Percent moles is not
the percent mass too. You must convert or die.
Example:
| Find the mass percent of each element of penicillin (C14H20N2SO4).
Answer
Here's a hint: if they don't give you how much there is, assume one mole.
So if there is one mole of penicillin, there must be 14 moles of carbon, 20 moles of
hydrogen, and so on.
To find the mass of each element in this mole of penicillin, just do the DA using the
g/mol conversion.
Mass of carbon = 14 moles C x 12.01 g / mol = 168.4 g.
Mass of hydrogen = 20 moles H x 1.008 g / mol = 20.16 g.
Mass of nitrogen = 2 moles N x 14.01 g / mol = 28.02 g.
Mass of sulfur = 1 mole S x 32.07 g / mol = 32.07 g.
Mass of oxygen = 4 moles O x 16.00 g / mol = 64.00 g.
The total mass can be found just by adding:
168.4g + 20.16g + 28.02g + 32.07g + 64.00g = 312.6 g
Percent mass is mass of one thing divided by the total mass, times hundred percent:
Percent mass carbon = 168.4 g / 312.6 g x 100% = 53.87%
Percent mass hydrogen = 20.16 g / 312.6 g x 100% = 6.449%
Percent mass nitrogen = 28.02 g / 312.6 g x 100% = 8.964%
Percent mass sulfur = 32.07 g / 312.6 g x 100% = 10.24%
Percent mass oxygen = 64.00 g / 312.6 g x 100% = 20.47%
And the percents add up to 99.993%, which is close enough to 100%. |
Go try some more percent mass practice
problems now!
Empirical and Molecular Formulas
The molecular formula is the type that we've always been using: H2O, C6H12O6,
C2H4, and all the like. It's how many atoms of each element are
present in one molecule of the substance. The empirical formula is the reduced form of
this. It's the ratio of atoms. For H2O, there's 2 hydrogens for every oxygen.
So the empirical formula is the same. However in C6H12O6,
there is a ratio of 6 : 12 : 6. That can be reduced, so the ratio is 1 : 2 : 1. Therefore
the empirical formula is CH2O. Likewise, the ratio 2 : 4 in the last one can be
reduced to 1 : 2. The empirical for it is is CH2.
Example:
| The empirical formula of a compound is found to be C2H3O4.
The molar mass was found to be 273.1 g / mol. Find the molecular formula. Answer
Let's find the molecular mass of the empirical formula.
12.01 g/mol x 2 + 1.008 g/mol x 3 + 16.00 g/mol x 4 = 91.04 g / mol.
And since the molecular formula is just a multiple of the empirical, let's see if 273.1
g / mol is a multiple of 91.04 g / mol.
273.1 g/mol / 91.04 g/mol = 3.000.
Sure enough, the number goes divides almost evenly three times. That means the
molecular must have three times the number of particles of the empirical. Multiplying each
by three gives the molecular formula to be C6H9O12. |
It's important to remember that the molecular formula is a multiple of the empirical
formula in both subscripts and molar masses.
Chemical Equations and Balancing Them
A chemical reaction is when one or more molecules rearrange their atoms to form new
molecules. Here is an example:
CH4 + O2 ---> CO2 + H2O
You can see this visually below:
|
+ |

|
-> |
Methane |
|
Oxygen |
|
|

|
+ |
 |
|
Carbon Dioxide |
|
Water |
The things on the left side are called the reactants, and the
things on the right are called the products. The reactants are generally
transformed into the products until one of the reactants runs out, or the system reaches
equilibrium (a balance).
As another example, if you wanted to say that two molecules combine to form one, just
use the coefficients. Just like in algebra, you can put numbers in front of the molecule
to show how many of them are in the equation. Let's say 2 of Molecule A and 3 of Molecule
B are needed to make 4 of Molecule C. The equation would look like:
2A + 3B ---> 4C
Another thing that's important to right down is what state each reactant and product
is, by little subscript letters. The symbols are:
- Solid: (s)
- Liquid: (l) (When you write it by hand, it's a lowercase cursive l.)
- Gas: (g)
- Aqueous (means dissolved in water): (aq)
So the first equation should have really been written as:
CH4 (g) + O2 (g) ---> CO2 (g) + H2O
(g)
It's funny how they teach you to do that, but on the AP test on the Equation Writing
section, they will not look for those symbols. But your teacher most certainly will, so
get into the habit!
That equation is better, but it still is missing a key point in chemical reactions.
Atoms cannot be created nor destroyed; they can only be put in different orders. If you
look above, there are two oxygens (green) on the left and three oxygens on the right.
Where did that extra oxygen come from? The key is to realize that these aren't one to one
reactions. That is, they all don't have coefficients of one. So you have to balance.
Let's start with hydrogen. There's four on the left and two on the right, so multiply
the molecule on the right by two:
CH4 (g) + O2 (g) ---> CO2 (g) + 2H2O
(g)
Now the hydrogens are balanced, but the oxygens aren't. Now we have 4 on right and 2 on
left. Multiply atom with oxygen on left by two:
CH4 (g) + 2O2 (g) ---> CO2 (g) + 2H2O
(g)
If you count them, everything adds up. There are the same number of atoms on the left
as on the right. That is the correct chemical equation.
Here is The Art of Balancing Instruction Manual, by none other than
Takalah:
| Before doing anything, check if it all adds up. If the same number of atoms
exist on both sides, then it's already balanced and you're done. If not, start your
balancing with the atom that is combined with another on both sides, and the one that has
the most atoms. You really do want to start with the most complex one. For instance,
in C2H5OH + O2 CO2 + H2O, you would
start with H first, because it's in a molecule with other atoms on both sides, and the
numbers of atoms (5 and 2) are greater than the other one that fits the first criteria
(C).
Leave the atoms that stand by themselves for last. Like in the equation in the
last rule, you would save O2 for last. Since changing the coefficient for this
only affects one atom, you can use it as a "finishing touch", balancing the
oxygens after all the other ones are done, but without messing another atom up.
Don't change the molecular formula!!! As frustrating as some of these
problems can be at first, don't be tempted to change one little number in some molecular
formula just to make something balance. Remember that changing the coefficient will just
change the number of particles that are involved in the reaction. Changing the subscripts
will change the whole molecule into something else. The molecule is a unit. So don't do
it! |
|
Example:
| Write balanced equations for the following: Glucose (C6H12O6)
reacts with oxygen gas to form carbon dioxide and water.
Indium reacts with oxygen to make indium (III) oxide.
AgNO3 (aq) + H2SO4 (aq) ---> Ag2SO4
(s) + HNO3 (aq)
Answer
- The unbalanced reaction is: C6H12O6 (s) + O2 (g)
---> CO2 (g) + H2O (g)
The most complicated atom is
H, since it's in glucose and water, and that the subscripts are the largest. Let's see;
there are 12 on the left and 2 on the right, so let's try multiplying right by 6:
C6H12O6 (s) + O2 (g) ---> CO2 (g)
+ 6H2O (g)
Now you move on to the next complicated atom; C, since it's in both carbon dioxide and
glucose. There are six on left, and one on right; try multiplying right one by 6. You get:
C6H12O6 (s) + O2 (g) ---> 6CO2 (g)
+ 6H2O (g)
Everything is basically done now, you got have to finish it by balancing oxygens using
the O2 molecule. There's 6 on left; and 6x2+6 = 18 on right. (Remember that you
have to multiply coefficient by subscript to get number of atoms.) So there must be 12
atoms on right to balance it. Twelve oxygen atoms is 6 oxygen molecules, so the final
answer is:
C6H12O6 (s) + 6O2 (g) ---> 6CO2 (g)
+ 6H2O (g)
- You have to remember the stuff you learned in the last part to do this. Indium (III)
oxide is In2O3. So the equation is:
In (s) + O2
(g) ---> In2O3 (g)
Start with the most complicated one, which is oxygen. Multiplying left by three and
right by two gives
In (s) + 3O2 (g) ---> 2In2O3 (g)
Now to balance In's, there are four total In's on right. So there must be 4 In's in
left. Answer is:
4In (s) + 3O2 (g) ---> 2In2O3 (g)
- AgNO3 (aq) + H2SO4 (aq) ---> Ag2SO4
(s) + HNO3 (aq)
This is the hardest one yet. Oxygen is too hard to do
right now, since it's in all four. Let's start with Ag, by getting two on left:
2AgNO3 (aq) + H2SO4 (aq) ---> Ag2SO4
(s) + HNO3 (aq)
That changes the N to 2N. Looking at the right, we have only one N. Let's multiply that
one by 2 too.
2AgNO3 (aq) + H2SO4 (aq) ---> Ag2SO4
(s) + 2HNO3 (aq)
Now we get 2 H's on the right, but that's favorable, since we have 2 H's on left. In
fact, if you find out how many oxygen's are on each side, you gots ten, and that's your
answer. Note that solving these can be like a chain reaction; solving for one gets you how
many of another, then you balance that, and it goes on.
|
Stoichiometric Calculations
One thing to realize when doing any calculations is that moles and coefficients are
interchangeable. Both mean number of particles, or multiples thereof. So in 2A + 3B
---> 4C, it either means 2 particles of A combine with 3 particles of B to make 4
particles of C, or 2 moles reacts with 3 moles to make 4 moles.
With that in mind, here is a simple problem.
Example:
| The formation of water from hydrogen and oxygen gas is: 2H2 (g) + O2
(g) ---> 2H2O (l). What mass of water will form from 12.0
grams of hydrogen and excess oxygen (assuming the reaction goes to completion?) Answer
First what you must do in any of these problems is get all given masses into moles. You
are given 12.0 grams of hydrogen, let's see how many moles that is:
12.0 g H2 x 1 mol / 2.02 g = 5.94 mol H2
So how much water is formed? According to the equation, for every 2 moles of hydrogen,
2 moles of water are produced, or in other words, a 1 to 1 ratio. So 5.94 moles of water
will be formed. The question asks for what mass, so we're not quite done yet.
5.94 mol H2O x 18.0 g / mol = 107. grams of H2O. |
The "oxygen in excess" is important. We're assuming that there's tons of
oxygen, enough to supply whatever the hydrogen needs. If there was only
.0000000000000000000001 moles of oxygen, 5.94 moles of water obviously can't form.
Let's try one more of this type before moving on to LRs.
Example:
| The newly discovered element Takalahium (symbol Tak; molecular mass = 411 g/mol)
combines with oxygen to form Takalahium Oxide. The unbalanced equation is: Tak + O2 ---> Tak2O3
How many grams of Tak Oxide are formed when burning 8.00 kilograms of Tak?
Answer
First and foremost, the balanced equation is needed. That would be:
4Tak + 3O2 ---> 2Tak2O3
Then convert all given masses to moles:
8.00 kg Tak = 8000 g x 1 mol / 411 g = 19.5 moles.
Since there are 2 Tak's for every 1 Tak Oxide, there must be half as many moles of Tak
Oxide, or 9.50 moles. You can also use DA to do the same mole ratios.
Before you can get grams, you must first find the molar mass of Tak Oxide, which is no
problem:
Mass = 2 x 411 g + 3 x 16.0 g = 870 g/mol.
Then you find the mass:
9.50 moles x 870 g / 1 mol = 8260 grams = 8.26 kilograms. |
In these last two problems, we always assumed that one of the reactants was in excess.
This simplified things, but it's often not the case in many reactions. You have given
amounts of each reactant. So how do you do this? Simple, just find out which out runs out
first molewise. The one that does is called the limiting reactant, or just LR. One quick
example:
Example:
Tak + Asdf ---> TakAsdf
You are given 45.0 grams of Takalahium (411 g/mol) and 500. grams of Asdfur (5620.5
g/mol). Find the limiting reactant in the formation of Takalahium Asdfite.
Answer
The limiting reactant isn't necessarily the one with the smallest mass. Remember that
reactions look at number of particles, not at mass. So let's get both of these values into
moles:
45.0 g Tak x 1 mol / 411 g = .109 moles.
500.g Asdf x 1 mol / 5620.5 g = .0890 moles.
As both are being consumed, you'll see that Asdf is used up first. Therefore it's the
limiting reactant, even though there is over ten times as much of it by mass. |
Note that mole ratios are important. Let's say 2 Tak's become 1 Asdf. Then it becomes a
little bit more than just finding the bigger number, but not very harder. You start with
one, say, Tak. Assume that it is the LR. Then, according to the mole ratio, you would need
at least half as much Asdf for Tak to become the LR. Do you have a half? Well, one-half of
.109 moles is about .05 something, and you do have that much. So if Asdf isn't your LR,
then Tak must be. (Of course if it was exactly equal to half, then you could use either
one, there would be no LR, and everything gets used up.)
What happens if you started with looking at Asdf? Well you need twice as much Asdf's.
Twice .0890 is .17 something. You don't have that much Tak, therefore Tak is your LR, no
matter how you look at it.
Once you find the LR, you can go ahead and finish the problem just like the others. So
what's the difference? Once you find the LR, you use that amount and throw away the
other amount. So like in the above example, you use the .0890 value, and forget about
the .109. Of course, if they ask you to refer to the original amount, such as how much
reactant is left over, then you need to use it. But not for stoich.
Example:
| In the previous example, how much Takalahium Asdfide is produced by the reaction? And
how much of each element is left over? Answer
Since the Asdf was the limiting reactant, with .0890 moles, you use this value for all
remaining stoich problems. .109 moles is not how much Tak reacts, it will be less than
that. Since it's a one-to-one ratio, .0890 moles of Tak will react with .0890 moles of
Asdf to form .0890 moles of TakAsdf. The question asks what mass was produced. That's
easy:
Molar mass = 411 g/mol + 5620.5 g/mol = 6031.5 g/mol,
.0890 mol TakAsdf x 6031.5 g / mol = 537 grams of TakAsdf.
As to the second prompt, you know that .109 moles Tak was initially present, and .0890
moles or Tak was consumed in reaction. A simple subtraction and conversion, and there's
your answer:
Moles left over = Moles initially there - Moles used up = .109 mol - .0890 mol = .020
mol.
.020 mol Tak x 411 g / mol = 8.22 g
As to the Asdf, all of it was used up, so there's 0 g left. |
Percent Yield
One little thing. You can test the above stuff in a lab, like measuring out the
reactants, and see if you get the calculated amount of product. You probably won't get the
exact number, but rather a number that's below it. There could be many reasons for it,
such as maybe the reaction doesn't go to completion, or maybe there's impurities or
something. The theoretical yield is how much you should get, according to stoich. The
actual yield is how much you actually get, determined in a lab. The percent yield is the
ratio of these two. The equation:

Yields are masswise. That is, how much you get is measured in kilograms, grams, mass.
Note that the percent yield will always be under 100%. The theoretical yield is the max
you can get. (You're not going to get more substance than calculations predict.)
Now it's time for the big example, that ties together balancing equations, stoich, LRs,
and percent yield.
Example:
| Here's the combustion of ethane (not balanced): C2H6
+ O2 ---> CO2 + H2O
32.0 g of ethane was burned with 15.0 grams of oxygen gas, and 10.8 grams of carbon
dioxide was formed. Calculate the percent yield of carbon dioxide.
Answer
Before doing anything, get the equation balanced!
2C2H6 + 7O2 ---> 4CO2 +
6H2O
(If you didn't know how to do that, review the rules of balancing. I do have a 20
megabyte limit here!)
Now to convert all given masses into moles:
32.0 g ethane x 1 mol / 30.0 g = 1.07 mol
15.0 g oxygen x 1 mol / 32.0 g = .469 mol
Which one is the LR? Let's look at ethane first. If ethane is indeed the LR, then the
moles oxygen reacted would be:
1.07 mol ethane x 7 mol oxygen / 2 mol ethane = 3.74 moles oxygen needed.
Since the oxygen will have run out first, oxygen is the limiting reactant. Disregard
the 1.07 mol.
Now to find the theoretical yield. 4 moles of carbon dioxide will form from 7 moles of
oxygen:
.469 mol oxygen x 4 mol CO2 / 7 mol oxygen = .268 moles.
Now to get the mass:
.268 moles x 44.0 g / mol = 11.8 grams.
That's how much you should get. But experiment shows that you get only 10.8 grams.
Finding theoretical yield:
10.8 grams / 11.8 grams x 100 % = 91.5% |
Copyright ©1999 by Takalah. All
rights reserved. This concepts portion was last updated on September 4, 1999